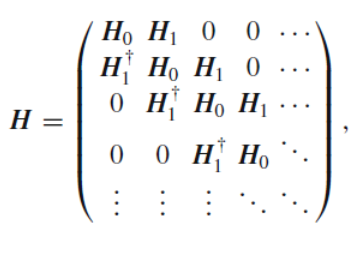I could not find a simple tutorial on creating block tridiagonal matrices online. So, here is a quick tutorial on how to achieve this using three custom N\times N matrices. This procedure may prove handy in several contexts in STEM-based calculations (ex: constructing tight-binding, and truncated frequency-space Floquet Hamiltonians).
The functions involved are numpy.matrix(), numpy.eye() (which is not needed if you just want to stick with numpy.matrix(), and numpy.kron().
import numpy as np
# Number of times to repeat the matrix that goes in diagonal, along the diagonal:
num_blocks = 3
# N x N dimensional blocks that go in the final tridiagonal matrix:
domestic_abuse = np.matrix([[1,1],[1,1]]) # Above diagonal
bullying = np.matrix([[3,4],[5,6]]) # Diagonal
death = np.matrix([[2,2],[2,2]]) # Below diagonal
# Positions of above blocks in the final matrix will be specified by the following matrices:
I_AM_OKAY = np.eye(num_blocks,num_blocks,k=1) # Above diagonal
FORREAL = np.eye(num_blocks,num_blocks) # Diagonal
THIS_IS_A_HEALTHY_COPING_MECHANISM = np.eye(num_blocks,num_blocks,k=-1) # Below diagonal
# It is instructive to see what each of the 6 matrices above look like on their own.
# If the np.eye() matrices above were to be other matrices,
# we could construct a block matrix of a different structure (i.e. not tridiagonal).
# For example, using I_AM_OKAY = np.matrix([[0,0,1],[0,0,0],[0,0,0]]) for num_blocks = 3
# would make the code skip the line above the diagonal. Try it!
# Finally, we use the Kronecker product to construct the tridiagonal matrix:
final_matrix = (np.kron(I_AM_OKAY, domestic_abuse)
+ np.kron(FORREAL, bullying)
+ np.kron(THIS_IS_A_HEALTHY_COPING_MECHANISM, death))655 views