This was the product of a group project that Joanne T.-Y. H., Benjamin S., Erik A. and I worked on for our PHYS 178 (The Biophysical Basis of Neurons and Networks) course. It was pretty neat trying to figure out how like-minded peers could collaborate on the same problem, and to present research updates periodically to others who didn’t necessarily know about our problem. While my first project was a mild introduction to theoretical study, this work made me start to realize that theoretical models are pretty darn cool. Anyways, here is a TL;DR for this project, followed by the Introduction and References sections of our final write-up for the course. Once I receive permission from all co-authors, I will include our results here.
TL;DR: We solved coupled ODEs associated with various modified Hodgkin-Huxley models and theoretically compared their effectiveness against new types input signals.
Excitability of Type III Neuron
Introduction
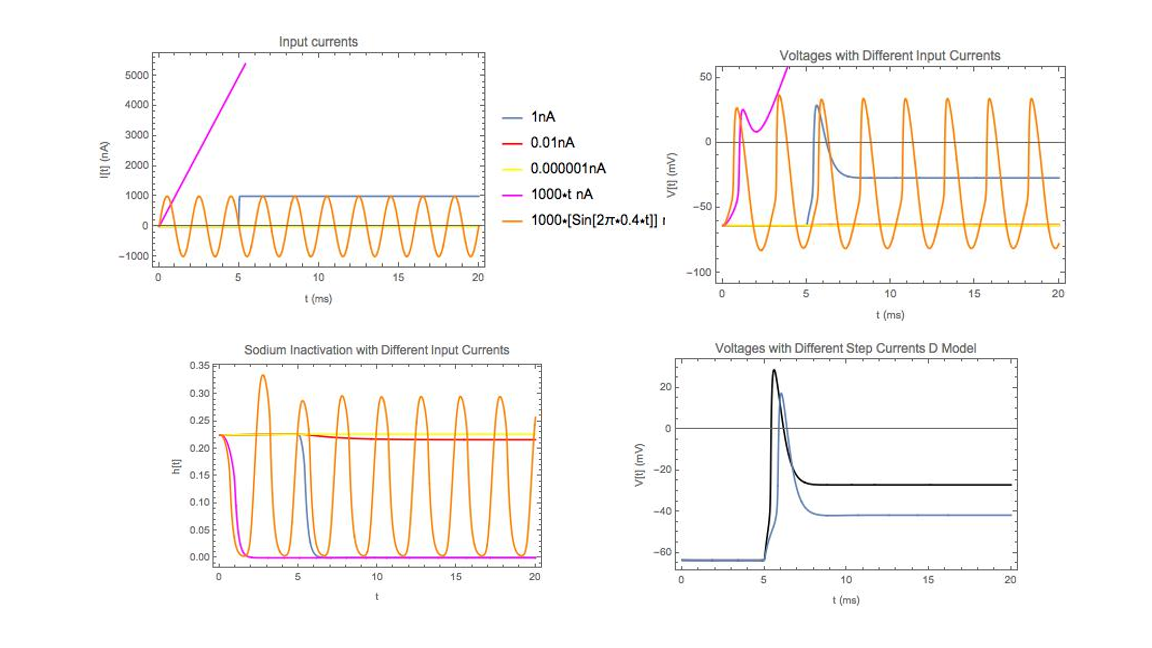
This paper will explore an attempt to reproduce the results of a paper by Huguet et al.: Phasic Firing and Coincidence Detection by Subthreshold Negative Feedback: Divisive or Subtractive, or Better, Both [1]. Huguet et al. model phasic neurons, which fire after activation by presynaptic input (which contrasts with tonic firing1which is often characterized by a steady action potential firing at a constant frequency, i.e. without presynaptic input [4]). Phasic neurons have high temporal precision for phase locking and coincidence detection, and are classified as Type III neurons. Type III neurons are fired at most once or twice (or not at all) regardless of stimulus intensity or duration; typically due to a fast-rising input (such as a step current) [1].
What controls phasicness is dynamic, voltage-gated negative feedback that can happen at subthreshold levels. This prevents neurons from spiking if increasing input doesn’t rise fast enough. There are two such negative feedback mechanisms that are responsible for phasicness: Subtractive (S) and Divisive (D). A combination of both S and D, the Combined mechanism (C), could be considered as well. The Subtractive mechanism results from an outward, low-threshold, Potassium current; while the Divisive mechanism results from an inward Sodium current with subthreshold inactivation. The Combined mechanism integrates both S and D into a mechanism that draws from both S and D. The general idea behind all mechanisms is that if a neuron depolarizes slowly, an activation/inactivation process develops faster than the depolarization so that it does not fire (and so is maintained at subthreshold levels).
A version of the Hodgkin-Huxley model modified for Type III neurons was used to model the S, D and C mechanisms (see section II. Method). Performance was assessed per the precision of phase-locking and coincidence detection given by the models’ responses to repetitive packets of excitatory synaptic inputs with varying temporal coherence.
Methods, Results and Conclusion

References
- Phasic Firing and Coincidence Detection by Subthreshold Negative Feedback: Divisive or Subtractive or, Better, Both, G. Huguet, X. Meng, and J. Rinzel, Frontiers in Comp Neuroscience 11 (2017): 3.
- Rothman, J. S., and Manis, P. B. (2003). The roles potassium currents play in regulating the electrical activity of ventral cochlear nucleus neurons. J. Neurophysiol. 89, 3097–3113. doi: 10.1152/jn.00127.2002.
- United States of America. National Institute of Health. The Brain: Understanding Neurobiology. U.S. Department of Health and Human Services, n.d. Web. 22 Mar. 2017.
- Phasic versus tonic dopamine release and the modulation of dopamine system responsivity: a hypothesis for the etiology of schizophrenia, Grace AA, PubMed PMID: 1676137.